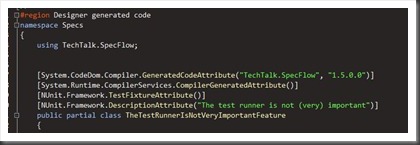
I answered a question on Twitter today from a guy who had problems running SpecFlow scenarios with MSTest. That shouldn’t be I thought to myself – in SpecFlow the test runner is only used for the auto-generated stuff (#2 in this pictures) and shouldn’t affect the code you write. Lets try it.
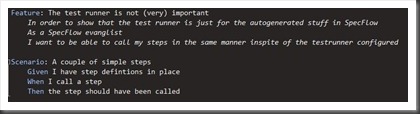
The default test runner is NUnit so first I simply create a new Specs-project and created the following scenario:
I then Nuget’d SpecFlow, Should and NUnit with these commands:
Install-Package SpecFlow
Install-Package NUnit
Install-Package ShouldFluent
And sure enough – when I compile some NUnit code is auto generated for me:
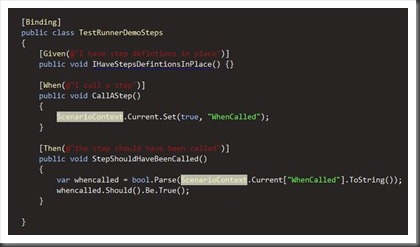
Just for good manners I implemented the steps and ran the specification. It worked with these (naïve) steps in place:
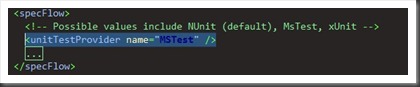
If I now change the app.config (added by NuGet install of SpecFlow) and configures it to use MsTest, like this:
And then add MsTest with a reference. Finally I save the scenario file which triggers the SpecFlow custom command for the file to run and generate the code. I now get the following code generated instead:
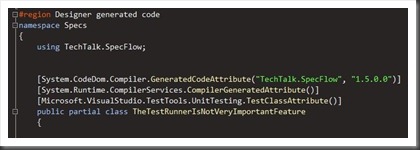
Sadly the test don’t run because I forgot the fact that in order to get MsTest to run the project they reside in need to be a test project but you get what I mean. Try to switch to xUnit or MbUnit for example.
Conclusion
So to sum up – the test runner in SpecFlow is not very important. It’s just the auto generated stuff. Your steps, SpecFlow attributes etc. will still be the same; it’s just being called by a different test runner.
Note that there’s not great use case for this – it’s just demoing that the test framework doesn’t matter much.